Basic Physics of Ultrasound Elastography
Maurizio Cè1, Natascha Claudia D’Amico2 and Michaela Cellina3
1Postgraduate School in Diagnostic and Interventional Radiology, University of Milan, Italy
2Data Scientist, IQVIA, Frankfurt, Hesse, Germany
3Department of Radiology, ASST Fatebenefratelli Sacco, Italy
Received Date: 14/11/2022; Published Date: 09/12/2022
*Corresponding author: Maurizio Cè, BA MD, Postgraduate School in Radiology, University of Milan, Via Festa del Perdono, 7, 20122, Milan, Italy
Abstract
Ultrasound Elastography (USE) or Elastosonography is a non-insasive ultrasound-based imaging method used to assess tissue elasticity. The different types of ultrasounds elastography are distinguished on the basis of the basic mechanisms for estimating elasticity. In strain imaging, mechanical stress (manual compression or acoustic pulse) is applied to the tissue and the resulting differential strain is used to infer the elasticity, in shear wave imaging the shear wave velocity is used. Shear waves can be produced using a vibrating mechanical device, as in Transient Elastography (TE), or an Acoustic Radiation Force Impulse (ARFI), which can be highly focused, as in the point-SWE (p-SWE), or directed to multiple zones in a two-dimensional area, as in 2D-SWE. A general understanding of these principles is important for clinicians to adopt adequate sampling protocols and interpret the data correctly.
Introduction
Ultrasound Elastography (USE) is a non-invasive imaging technique that uses the physical properties of ultrasound to evaluate the elasticity (or, conversely, the stiffness) of different biological tissues in order to obtain diagnostic information [1]. In fact, not only the elasticity of the adipose tissue is different from that of the glandular tissue, but the normal glandular tissue has different mechanical properties from the neoplastic glandular tissue. Intuitively, this is also why clinical palpation is such an essential tool for detecting and locating large tumor masses during physical examination.
In the first paragraph we explain the physical principles underlying the USE and its various sub-techniques. In the second part of the article some examples of clinical applications such as liver, breast, thyroid and lymph nodes are briefly presented. For each application, some studies are reported that illustrate how the USE could usefully integrate B-mode ultrasound into clinical routine, contributing to the paradigm shift from a qualitative ultrasound approach to quantitative multiparametric ultrasound. Although the USE has gained a lot of popularity in recent decades, low specificity and operator dependency are the main problems preventing large scale application [2]. Therefore, in the last paragraph, we present some recent findings of how the application of artificial intelligence to the USE could partially overcome these limitations, improving the diagnostic performance of this imaging technique and its integration into the clinical workflow.
Basic Physics of Ultrasound Elastography
The physical principles of the USE techniques are complex; in-depth reviews are available here [3-5]. In this article, we propose a description for clinicians using simplified models and avoiding as much as possible the differential notation in the equations. We are aware of the several limitations of our description of physical principles from a formal standpoint, but we tried to achieve a good balance between correctness and accessibility of contents, especially for those without advanced mathematics knowledge. Similar accounts may be found in other reviews [1,2,6].
Longitudinal elasticity and young’s modulus (E)
To introduce the physical principles underlying USE techniques it is useful to start considering the first developed technique, which is classified as strain elastography (SE) [1,7-10].
SE measures the stiffness as a function of tissue deformation generated by applying pressure with a probe on the body surface [1,2,10]. In the studies adopting this technique, researchers are interested in knowing a quantity defined as Young's modulus (E), which expresses the tissue property of our interest, namely its elasticity.
In material mechanics, the elasticity of a material describes its tendency to resume its original size and shape after being subjected to a deforming force or stress [11].
The stiffness is the opposite of elasticity and is the ability of a body to oppose the elastic deformation caused by an applied force [12]. A more detailed account of the elastic properties of tissues may be found here [13].
Since stiffness is the resistance to deformation, an application of external force is required to measure it: this is, in very simple terms, the underlying principle of SE.
If an elastic body is not free to move when it is subjected to an external force, it deforms and develops a force that opposes the deformation. Hooke's law is the simplest law describing the behavior of an elastic spring subjected to a force F longitudinally, either in traction or compression (Figure 1). Hooke's law states that an elastic body undergoes a deformation directly proportional to the force applied to it:
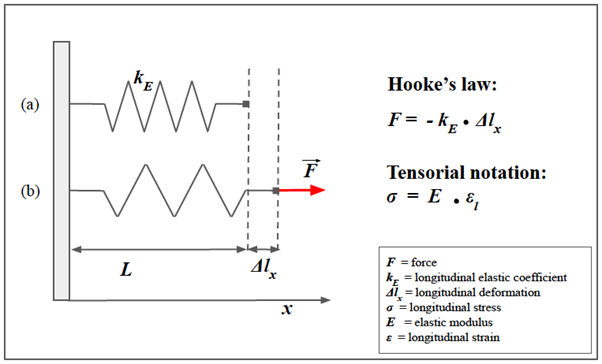
Figure 1: Spring model of Hooke’s law and longitudinal strain.
A simple helical spring model can be used to represent Hooke’s law. Hooke's law states that the force (F) required to extend or compress a spring for a certain distance (Δlx) scales linearly to that distance. On the left, the upper image (a) represents the spring in rest conditions, characterized by a longitudinal elasticity constant kE that is typical of the spring. The lower spring (b) represents the spring stressed in traction by a force F parallel to the x-axis. Δlx represents the longitudinal displacement of the free hand of the spring. In this notation, note the "-" sign in front of the second member: that means that F is the restoring force exerted by the spring on whatever is pulling its free end, since the direction of the restoring force is opposite to that of the displacement. Under Hooke's law there is also the tensor notation with the stress (σ) in the place of the force (F), and the longitudinal deformation (εl) in the place of the displacement (Δlx).

where is the force of retraction of the spring that is equal and opposite to the applied force, represents the elongation undergone by the spring along the -axis (we suppose that the deformation occurs only in 1-D), and represents the longitudinal elasticity coefficient, which depends on the nature of the material itself and is dimensionally expressed as [N.m-1]. This law is valid, of course, within certain limits, beyond which the body loses the capacity to return to its original shape (elastic behavior) and becomes permanently deformed (plastic behavior).
The formulation of Hooke's law in Equation 1 is useful for describing the deformation of a spring stressed longitudinally, in traction or compression, along the -axis. Here we present a more general formulation of Hooke's law using a tensorial notation that uses two vector quantities: the tension (equal to external force per unit area) and the strain (equal to deformation per unit length):
where is the force of retraction of the spring that is equal and opposite to the applied force, represents the elongation undergone by the spring along the -axis (we suppose that the deformation occurs only in 1-D), and represents the longitudinal elasticity coefficient, which depends on the nature of the material itself and is dimensionally expressed as . This law is valid, of course, within certain limits, beyond which the body loses the capacity to return to its original shape (elastic behavior) and becomes permanently deformed (plastic behavior).
The formulation of Hooke's law in Equation 1 is useful for describing the deformation of a spring stressed longitudinally, in traction or compression, along the -axis. Here we present a more general formulation of Hooke's law using a tensorial notation that uses two vector quantities: the tension (equal to external force per unit area) and the strain (equal to deformation per unit length

where σ represents the tension applied, represents the strain and represents a constant known as Young's modulus, which, similarly to the in Equation 1, depends on the intrinsic characteristics of the body.
Although Equations 1 and 2 look similar, they are not equivalent. The demonstration of Equation 5 is beyond the scope of this text, however, in simplistic terms, we can define the tension as the ratio between the applied force and the surface on which the force is applied:
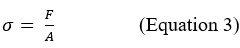
Its unit of measure is the Pascal, dimensionally defined as .
In turn, the longitudinal strain is defined as the ratio between the change in length and the initial length:

where lf is the final length and li is the initial length (or L). εl is also called the longitudinal deformation coefficient and, unlike the displacement Δlx in the simplified Hooke's law (Equation 1), it is a dimensionless quantity.
In this second formulation (Equation 2), Young's modulus (E) appears in the place of the longitudinal coefficient of elasticity (kE) in Equation 1. Young's modulus of elasticity expresses the relationship between the stress and the deformation (strain) in the case of uniaxial load conditions and in the case of fully elastic behavior of the material:
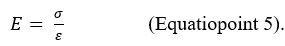
Shear waves and shear modulus (G)
Ultrasound propagate through compression waves longitudinally, in the same direction of the tissue displacement induced by an external force applied perpendicular to the surface. In shear waves, the particles propagate orthogonally to the direction of the ultrasound beam [7-9] (Figure 2). Unlike strain elastography, in which Young's modulus is derived from the displacement, in shear waves methods, the physical quantity of interest is the shear waves speed. Young's modulus may then be converted from the shear wave velocity using Equation 2, on the assumptions of constant density, homogeneity, isotropy, and incompressibility of the material [7-9].
To understand the mechanisms underlying shear waves elastography, consider a cylindrical model, such as the one shown in Figure 2, which represents a portion of tissue. Up to now we only have considered the deformation that occurs along the force axis (longitudinal strain); however, in the absence of volume variations, a cylindrical object becomes thinner and wider when compressed. Consequently, it is possible to calculate not only the longitudinal strain εl but also the transverse strain εs. The percent change in the radial direction εt is called transverse strain and, analogously to the longitudinal strain in Equation 2 is defined as:
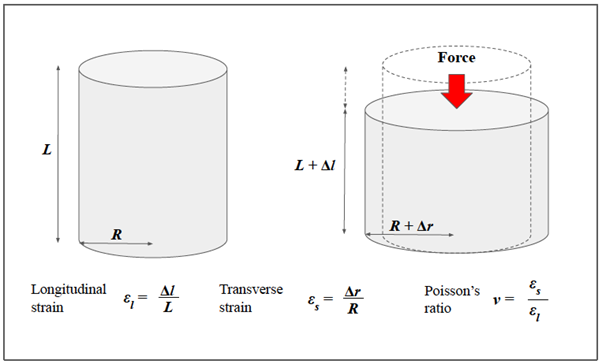
Figure 2: Relationship between the longitudinal and the transverse strain in solids: a cylindrical model.
The figure presents a cylindrical model representing a portion of biological tissue. Before compression, the cylinder has height (L) and radius (R). After the application of an orthogonal force (red arrow), the cylinder becomes thinner and wider. The longitudinal strain (εl) is defined as the ratio between the change in length (ΔL) and the initial length (L). The transverse strain (εs) is defined as the ratio between the variation of the radius (Δr) and the initial radius (R). The ratio between the longitudinal and transverse deformation is called Poisson's ratio and depends on the characteristics of the medium.
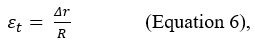
where Δr represents the change in width and represents the initial radius. Since the two components coexist, it is possible to calculate the ratio between the longitudinal and transverse deformation. This ratio is named Poisson’s ratio and is indicated with the Greek letter v ("ni"):

Poisson ratio is important as it represents the degree to which the material shrinks or expands transversely in the presence of longitudinal stress. In addition, Poisson's ratio indicates the extent of volume change caused by deformation that, in the case of a virtually incompressible material, has a value equal to 0.5. This is important because biological tissues react to compression more similarly to our cylinder than to the spring in Figure 1.
In the cylinder example, we considered transverse deformation as a result of longitudinal compression, and that model is important to understand how the two types of deformations are related. However, it is possible to consider a simplified model in which only shear forces act, such as the one in Figure 3. Similar to what has been done for Young’s Modulus, it is possible to describe a quantity, which we define G, to indicate the shear modulus. The equation becomes:
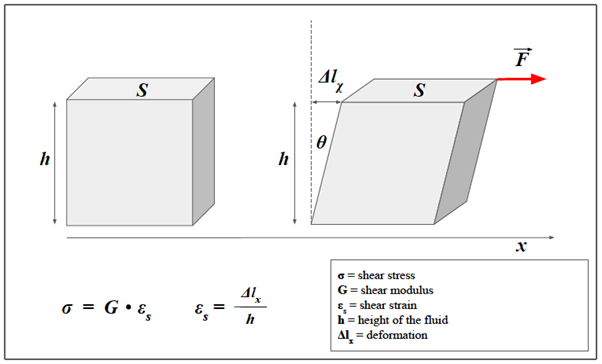
Figure 3: Shear strain in a solid.
Unlike the cylindrical model, the model in the figure allows us to consider the case in which only shear forces are acting. We consider a prism of elastic material and a shear force F (red arrow) applied parallel to the x-axis. Similarly to what was done for Young's modulus, it is possible to describe a quantity, which we define G, to indicate the shear modulus, that is the constant of proportionality between the shear stress and shear strain. The transverse deformation can also be expressed as a function of the angle θ.

where σ is the tangential (or shear) stress, is the shear modulus and represents the shear strain (i.e. the percentage of transverse displacement).
The two types of elastic moduli are not independent, but are interrelated, as seen from the Poisson ratio concept. Concerning the shear modulus, it is usually considered a derived parameter, which can be expressed through the elastic modulus (the "Young's modulus") and the Poisson's ratio. Thus, the transverse modulus of elasticity or shear modulus G can normally be calculated from the other two parameters through:

which, by making E explicit becomes:

Due to the high-water content of biological tissues, the Poisson's ratio can be approximated to 0.5 compared to an incompressible medium, from which:

These elastic modules are important not only because they define the deformations of bodies subjected to a force, but also because they influence the speed of propagation of mechanical waves in the medium.
For a sound wave, the longitudinal propagation speed is given by:
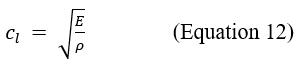
which E represents Young's modulus and represents the density of the medium. In soft tissues, the speed of sound is about 1540 m/s and is comparable to that in water (1500 m/s).
If we consider the speed of the waves propagating in the transverse direction (shear waves), the notation becomes:

where G represents the shear modulus and represents the density of the medium.
Equations 12 and 13 indicate that the velocity of propagation of longitudinal and transverse waves increases with the increasing of E and G, respectively. Because Young's modulus is always higher than the shear modulus (approximately three times the shear modulus, Equation 11), the longitudinal waves are always faster. The speed of the shear waves in the soft tissues (1-10 m / s) is significantly lower than the longitudinal waves and covers a wider range of values. This fact has important implications in USE because the differences in the speed of the shear waves can be used to obtain information on the elasticity of the tissues (see further).
In conclusion, the greater the value of E or G (that is to say, the greater the stiffness of the tissue), the greater the velocity of sound waves.
Viscoelastic models
Up to now, we have considered biological tissues as solids characterized by a perfectly elastic behavior, without considering the viscous components. In reality, biological tissues are highly hydrated media and internal friction forces cannot be neglected. Because biological tissues contain both elastic and viscous components, they are called viscoelastic media. Similarly, to elasticity, the viscosity of a viscoelastic material consists of two contributions: the shear viscosity, which is the ratio between the shear stresses and the deformation rate, and the elongational viscosity (or extensional viscosity), which is the ratio between the normal stresses and the strain rate.
When shear stress is applied to a fluid, instead of the deformation (as for the solid in Figure 3), it produces a sliding of the various layers of fluid (Figure 4). This sliding is hindered by internal frictional forces, a characteristic called viscosity. The dynamic viscosity of a fluid is a measure of its resistance to flow when tangential stress is applied and it is due to adjacent layers of fluid moving at different speeds. Shear elasticity in solids and viscosity in fluids are somehow interconnected, but with differences. In fact, viscosity is a property that manifests itself in a liquid in relation to the speed with which stress is exerted.
The model presented in Figure 5 (Kelvin-Voigt model) is used to predict the behavior of solid viscoelastic materials when viscosity is taken into account. Where the speed of the applied external force is slow (such as manual compression), the effect of viscosity can be ignored. Conversely, if a high-frequency vibration is applied, the viscous component will have a greater effect, the magnitude of which will depend on the frequency. Velocity dispersion caused by the viscosity occurs during wave propagation when the frequency is high in soft tissues, and viscosity must be considered [9].
When the Kelvin-Voigt model is used, the following equation is derived for the speed of a transverse wave instead of Equation 13 [9,16]:

Figure 4: Viscosity.
The figure illustrates the concept of viscosity and highlights the similarities with the shear stress in a solid. In the image, a plate flows on the surface of a fluid. The plate is pulled with a force of intensity F (red arrow). If there were no friction, the plate would move with a uniformly accelerated motion, however in reality its speed tends to be constant over time since the force F is balanced by a friction force due to the sliding of the various layers of liquid (in conditions of laminar motion). The viscous friction force acting on the plate has an intensity given by the relation 1 and it is directly proportional to the sliding speed. According to relation 2, it’s worth noting that unlike the shear stress in solids (3), the shear deformation is not expressed as a length, but as a gradient of velocity, that is the change in velocity with respect to the depth of the liquid.

Figure 5: Kelvin-Voigt model for viscoelastic materials.
Typically the Kelvin-Voigt model is used to predict the behavior of solid viscoelastic materials. This model is represented by a purely viscous damper (bottom) connected in parallel to a purely elastic spring (top). The constitutive equation associated is represented on the right. For more explanation, see text.
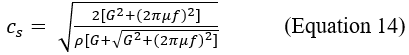
where G is the shear modulus, is the dynamic viscosity coefficient and f is the frequency. Despite the complexity of this equation, it is worth noting that shear waves velocity becomes a function of frequency f, and the higher the frequency, the faster the speed [8]. This could lead to differences in shear wave speeds measured within different imaging devices.
From Basic Physics to Imaging
From Young’s modulus to strain imaging
Strain imaging was the first type of USE developed in the 1970s by Dr. Jonathan Ophir [1,7]. In this technique, stress is applied perpendicularly through different modalities and the normal strain is measured to infer tissue elasticity [1,2].
Strain imaging is divided into two different techniques based on the modality of the compression: Strain Elastography (SE) and Acoustic Radiation Force Impulse (ARFI) strain imaging. In SE, compression is achieved directly, through manual compression or, indirectly, through heart pulse or respiratory movements [2]. In freehand compression, the ultrasound probe has the dual function of the ultrasound transducer and mechanical actuator [7]. The operator manages the transducer to produce a quasi-static load with a compressive stress of up to 3%-5% [2].
In ARFI strain imaging, the tissue deformation is produced through a short-duration (0.1-0.5 ms) high-intensity (spatial peak pulse average = 1400 W/cm2, spatial peak temporal average = 0.7 W/cm2) acoustic “pushing pulse” to produce a small displacement of ~ 10-20 μm in the normal direction (i.e. perpendicular to the surface) [2,14-17]. In this technique, the same transducer is used to generate and monitor tissue displacement. Intuitively, the displacement response is directly related to the magnitude of the applied force and inversely related to the tissue stiffness.
In both techniques, only the displacement in the direction of the impulse propagation is measured to calculate the strain, without taking into account transverse strain. In SE, the stress applied manually or physiologically is not quantifiable, but, assuming that the normal solicitation σ is uniform, Equation 2 is used to provide a quantitative assessment of Young's modulus and thus the elasticity of the tissues [1,2].
The induced tissue displacement is measured through different techniques depending on the manufacturer, including spatial-correlation methods, Doppler processing, or a combination of the two methods [1,2]. As known, the ultrasound image in B-mode consists of a 2-D map of signs representing the echos pattern or speckles pattern. In the first method, the elasticity is measured starting from the analysis of the images before and after the compression and by mapping the differences in the echo pattern within a region of interest (ROI). This method is called the spatial correlation method and measures 1D-displacement along the beam axis [1,2]. The cross-correlation coefficient is the mathematical tool used to evaluate the degree of similarity before and after the compression, but its analysis is beyond the scope of this text [1,2]. Here, we offer a simplified model of the functioning of SE using spring models to represent biological tissues (Figures 6a-c).
The autocorrelation-based method is the preferred estimator without considering the lateral displacement [18]. In reality, each ROI also moves in the transverse direction due to the lateral deformation of the tissues, therefore an adjustment is needed to estimate the displacement more accurately in both longitudinal and transverse directions. The second technique is essentially based on the same principle used in color-Doppler imaging [1,2,6]. In this case, the phase difference between the echo signals obtained by transmitting repeated pulses before and after compression is detected, and an autocorrelation method is used to calculate the displacement [1].
The methods described so far are not suitable for real-time processing because of the amount of computation time required. Concerning the practical application in the clinical setting, as the fluctuations in compression speed are large when manual compression is used, a high degree of accuracy to accommodate small displacements is required. More recently, some authors developed a new tool called the combined autocorrelation method (CAM), which combines the merits of the spatial correlation method and the phase differences detection [1, 19].
In SE, the numerical values that express the deformation and therefore the stiffness, are displayed as a semi-transparent color map called the elastogram, which is usually displayed on a superimposed B-mode image. Typically, low tension (hard tissue) is displayed in blue, and high (soft tissue) is displayed in red, although the color scale may vary depending on the manufacturer, clinical setting, or personal preferences [1,2,20,21].
In Strain Imaging, results are generally expressed as a Strain Ratio, a parameter normally used to measure the stiffness of a discrete mass lesion. In Strain Ratio, two regions of interest (ROI) are drawn on the target region and an adjacent reference region that is experiencing a similar stress. Then, a strain ratio is automatically calculated by the machine as the mean strain in the reference (B) divided by the mean strain in the “lesion” (A) [22]. Both ROI should be placed at the same depth.
Strain Ration (B/A) = Mean strain of fat area (B)/Mean strain in lesion of interest (A)
The usefulness of this index emerges, for example, in the evaluation of nodular lesions in which the probability of malignancy increases as the deformation ratio increases [23].
In strain imaging, the elastic modulus E is derived directly from the strain (Equation 2) and not from the differences in longitudinal waves speed (Equation 13). The reason is that the longitudinal waves propagate at a very high speed in biological tissues, with little variation between different types of tissues, and the relatively small differences do not allow adequate tissue contrast resolution for elastography measurements [1]. This does not apply to the speed of the shear waves, which is the basis of shear wave imaging [1].
A a good practical guide written by industry experts on how to perform deformation elastography is available here [22].
From shear waves to shear wave imaging
Shear wave imaging focuses on the shear waves created by the mechanical excitations in solids, in which the particles move perpendicularly to the direction of propagation [8,9]. As previously mentioned, the propagation speed of the shear waves in soft tissue is several orders of magnitude slower than the speed of sound waves in soft tissue and ranges from 1-10 m/s compared to 1540 m/s. For this reason, measurement of the shear wave speed is suitable for producing a good contrast resolution for soft tissues. In shear wave imaging Young's modulus E is calculated from shear wave speed. In fact, starting from Equation 9 and by making G explicit, we obtain

but (Equation 11) from which it derives:

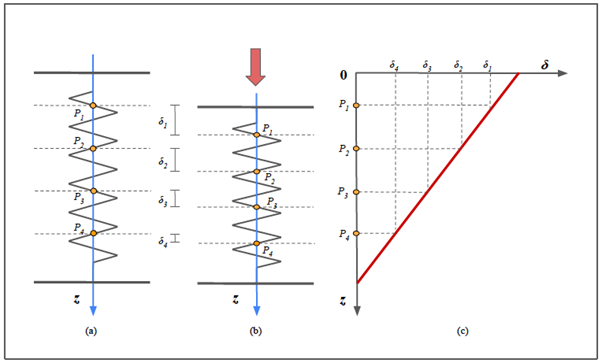
Figure 6a: Principles of strain elastography.
Assuming that the tissue behave as a purely elastic material and that the displacement occurs only in the longitudinal direction, the deformation can be approximated with a 1D spring model.
Before the compression (a), 4 different points (named P1-P4) located at different depths (z) are identified on the spring.
After the compression (b), each point displaced downwards (δ), but the more superficial show a greater displacement than the deeper ones (δ1> δ2 , δ2 > δ3 and so on).
Intuitively, the displacement is maximum for a point located at the free end of the spring (on the surface of the tissue) and virtually zero for a point located at the anchor end.
The graph in (c) represents the relationship between the depth (z) and the displacement. The relationship is linear and the displacement reaches the maximum for the more superficial points and tends to zero for the deeper ones. The slope of the line is an expression of the coefficient of elasticity, an intrinsic characteristic of the medium (see also Figure 10b).
Because two distinct points can hypothetically belong to areas with different elasticity coefficient, to assess the whole elasticity profile of the tissue it is necessary to correlate the displacement of different samples of neighboring points (see also Figure 10c).

Figure 6b: Principles of strain elastography.
The first row shows three spring models, representing different samples of biological tissues. Before the compression, they have the same initial length (Z), represented with the dotted gray silhouette superimposed. Assuming that the stress (σ=F/S) exerted on them (red arrows) is identical in all three cases, the tissue on the left demonstrates the greatest stiffness (blue spring), the middle one has intermediate stiffness (blue spring) and the one on the right is the most elastic (green spring).
In each spring we depicted four representative points (yellow dots) and before the stress those points are supposed to be virtually aligned.
The three graphs below represent the relationship between the depth of the points (with respect to the free end of the spring) and the displacement obtained. If we consider three points located at the same depth, for example the most superficial ones, the higher the stiffness of the spring, the less the displacement.
It is evident that the slope of the line is an expression of the coefficient of elasticity and it is an intrinsic characteristic of the medium.

Figure 6c: Principles of strain elastography.
The spatial correlation method measures 1D-displacement along the beam axis. Because the window moves while maintaining its speckle pattern as long as the strain is extremely slight, the displacement is calculated by setting a region of interest (dotted line), and calculating the spatial correlation of the speckles before (t’) and after (t’’) the compression. Displacement δ(z) in each site z in the beam direction of the tissue is then obtained through the correlation between the echo signal before and after the compression (the equation is not provided here, see [1,2]). In In the next step, the strain ε is obtained by considering the ratio of the difference in displacement between two points and their distance pre-compression. Young modulus is finally provided through Eq. 2 assuming the stress to be uniform.
The model in figure helps to visually understand the mechanism. We only consider the displacement in the direction of the propagation of the ultrasound beam. The tissue deformation is approximated using a 1D spring model as in Figure 10-11, but instead of the spring is represented an echo pattern similar to A-mode ultrasound. We consider four P-points located at different depth (z), named from 1 to 4. Point 1 and 2 are both located in a very elastic part of the tissue (in red). Taking into account their differential displacement (displacement in relation to the depth), the interpolating line in the upper right graph represent the elastic behaviour of that part of the tissue. Points 3 and 4 are both located in a rigid zone and therefore the differential displacement between the two points is different (note the different slope in the graph). In other words, even after correcting for depth, points P3-4 moves proportionally less than P1-2. In the graph in bottom right is depicted the displacement and longitudinal strain.
where cs measurement of allows estimation of E and G. Density ρ has units kg/m3 and cs has units m/s so pcs2 is dimensionally defined as kg/(m*s2) which is equivalent to N/m2 or kilopascals, that is the unit of measurement of E and G. A recent consensus advocates reporting results as shear wave speed in m/s as part of a standardized approach [1,24].
From a technical point of view, the calculation of the shear wave speed makes use of so-called time-of-flight (TOF) methods that perform a linear regression of the wave time arrival with respect to different positions [1]. The TOF indicates the measurement of the time taken by an object, a particle or a wave to travel a certain distance in a given medium: knowing the distance between the two points and the time taken to travel it, it is possible to derive the speed.
In shear wave elastography (SWE), the shear wave speed within a location of interest is derived by cross-correlating the time profiles of the shear wave-induced displacement at two neighboring points. Starting from the comparison of these profiles, a mathematical function gives the time taken for the shear wave to travel between the two points and then the shear wave speed is obtained by dividing the distance between the two points by the transit time [25]. TOF-based methods employ assumptions about tissue behavior to generate an estimate of the shear wave velocity, including local homogeneity, and a known direction of propagation [1].
As with strain imaging, shear waves can be generated by different sources, including external vibration and acoustic radiation force [1]. There are currently three technical approaches for SWE: 1) 1-dimensional transient elastography (1D-TE), 2) point SWE (pSWE)), and 3) 2-dimensional SWE (2D-SWE).
The first commercially available ultrasonic shear wave measurement system was the FibroScanTM (Echosens, Paris, France), which uses the probe as a mechanical actuator [26]. The probe produces a controlled mechanical excitation through a piston that punches the surface of the body at a high frequency and is integrated with an ultrasonic transducer to monitor the impulse of the shear waves generated by the piston. This method was designed specifically to measure liver stiffness and does not provide a 2D-guide for the operator, similarly to A-mode imaging. Therefore, the sampling relies on the operator's knowledge of the gross anatomy of the liver.
The analysis of the echo pattern along the A-line allows adjustment of the acoustic window avoiding the suboptimal ones due to the interference of vascular structures or other causes. In transient elastography (TE) the ultrasound transducer has a fixed focal configuration and uses the same probe to create the dynamic stress and to measure the shear wave speed along the A-line that is investigated by the transducer. The FibroScanTM displays the corresponding Young's modulus. However, the lack of grayscale images makes it difficult to understand where the measurement is being made, the need to recalibrate the spring in the device at intervals of 6 to 12 months (depending on the type of probe), reduced applicability in cases of obesity and impossible to employ in patients with ascites [27].
The second method is the pSWE. In this technique, an acoustic radiation force is used to induce tissue displacement in the normal direction in a single focal location (therefore named “point” SWE) [1,28]. However, unlike ARFI strain imaging, the tissue displacement itself is not measured. Similar to other SWE methods, the speed of the shear waves, which propagate perpendicularly to the direction of propagation of the ultrasound beam, is measured. Velocity may be either reported or converted in young’s modulus E to provide a quantitative estimation of tissue elasticity. Unlike TE, p-SWE may be performed on a conventional ultrasound device and B-mode image guidance is possible during the measurement because the same probe is used to generate the shear waves and to detect their propagation (Figure 7) [29].
In pSWE the tissue region interrogated by a single, highly-focused ultrasound beam is narrow because the shear waves rapidly attenuated by the internal frictional forces as they propagate from the excitation region. To derive tissue stiffness over a larger ROI, data from multiple pushes must be combined and this is the basis of 2-dimensional shear wave elastography (2D-SWE) [1,2].
2D-SWE is the latest technical innovation that uses acoustic radiation force to assess tissue elasticity (Figure 8). 2D-SWE alternates multiple perturbations and reading phases, enabling an image of the shear wave speed for a larger tissue sample. Instead of a single focal location, multiple focal zones are interrogated in rapid succession, faster than the shear wave speed. The need to transmit multiple pulses in sequence to synthesize a single elastographic image results in an increase in acquisition time. In order to achieve a larger ROI without increasing the acquisition time, some devices transmit multiple thrust beams at the same time, each constituting an independent source of shear waves [25]. As they propagate, the wavefronts generated by each thrust eventually meet and pass through each other. The combined wavefronts can assess a much larger region of tissue in a single transmission event. This creates a near cylindrical shear wave cone, allowing real-time monitoring of shear waves in the transverse direction for the measurement of shear wave speed and the generation of quantitative elastograms [1,6,25].
In 2D-SWE, a TOF algorithm is used to estimate the local shear wave speed at every location in the shear wave elastography ROI. The speed within a location of interest is derived by correlating the displacement induced by the shear waves at two neighboring points. The cross-correlation function also provides the correlation coefficient, which is used to assess the quality of the measurement.
The quality of the measurement is important in clinical practice. Some devices currently provide a tool called “confidence map”, helping the operator to check the quality of the sampling in real-time [30] (Figure 9). The confidence map displays an ROI identical to the one of the elastogram to chromatically represent the quality of the measurements in 2D. In the confidence map, the areas where the quality is lower than the required threshold will appear transparent, while the areas where values exceed the threshold will be depicted with different colors, depending on measurement quality. On the other hand, the elastogram will provide a chromatic map of elasticity values according to the confidence map, without accounting for the areas below the threshold. The operator can easily work with the split-screen modality, placing the ROI of the confidence map and the ROI of the elastogram side by side to select the most suitable tissue areas for the sampling, improving the quality of the examination (Figure 9).
Compared to pSWE and TE, the advantages of this technique include real-time visualization of a color quantitative elastogram superimposed on a B-mode image, enabling the operator to be guided by both anatomical and tissue stiffness information [31-33]. The optimal depth for sampling is considered 4-5 cm from the skin, although most vendors allow measurements to 8 cm from the transducer, it is proven that accuracy decreases below 6 cm because of attenuation of the ARFI pulse [2].
Figure 10 summarizes the different types of USE and some of the commercial devices currently available.

Figure 7: Point Shear Wave Elastography.
Image is obtained with Point Shear-Wave Elastography (ElastQ, Philips), using a convex probe in a healthy volunteer. A small ROI is placed in the middle third of the renal parenchyma. The mean stiffness value was 9.95 kPa.
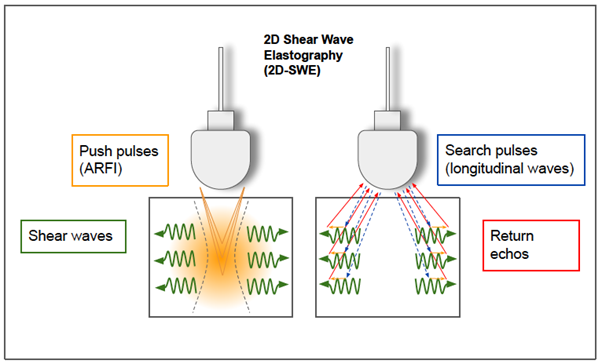
Figure 8: 2-D shear wave elastography.
In 2D-SWE, instead of a single focal location as in ARFI strain imaging and pSWE, acoustic radiation force is used to interrogate multiple focal zones in rapid succession, faster than the shear wave speed. In step 1 (on the left), shear waves are generated using acoustic radiation force impulses; they propagate perpendicularly to the primary US wave at a lower velocity. In step 2 (on the right), fast longitudinal wave excitation (blue and red arrows) is used to track displacement (orange small arrows) as shear waves propagate through a speckle tracking algorithm. In step 3 (not shown), tissue displacements are used to calculate shear-wave velocity (cs) with a time of flight algorithm and then shear modulus (G) is derived.

Figure 9: Confidence map and elastogram in 2D-SWE.
The image is obtained with two-dimensional shear-wave elastography (2D-SWE) (ElastQ, Philips), using a convex probe in a healthy volunteer. The confidence map is displayed on the left, setting a threshold of 60%. A standard deviation 60% or less of the mean value is indicative of a good quality acquisition. The areas of low quality (red) are filtered out by the system and displayed transparent (note that the area in red correspond to a vascular structure on the B-mode); the yellow color is a warning indicating that the area is not of good quality; the green indicates a good quality of the measurement. On the right, the elastogram depicts a colorimetric map of the stiffness in which blue color corresponds to greater elasticity while red represents greater stiffness. In the elastogram on the right a circle sampling area was inserted to obtain a quantitative measure of the stiffness value in the selected location (mean kPa 4.83). The presence of the confidence map helps the operator to check the quality of the sampling in real-time.
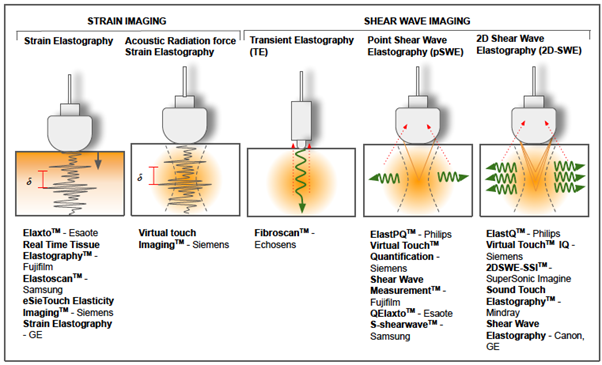
Figure 10: Different techniques of ultrasound based elastography and some of the commercial devices currently available.
Conclusion
Elastosonography is a powerful non-invasive method for the assessment of tissue stiffness which includes a set of different techniques depending on the principles used for elasticity estimation. In this review, we provided a brief introduction to the basic physical principles that underpin ultrasound elastography imaging. Although USE is a promising method, both investigator-dependent and independent factors may affect elasticity measurement. A general understanding of the underlying principles could benefit the entire process of data acquisition and interpretation, enhancing USE reproducibility and proper integration into the clinical workflow.
Disclosures
Funding: none.
Conflict of Interest: nothing to declare.
Ethical approval: not needed.
Informed consent: written informed consent was acquired before performing the examination.
Author contribution
Maurizio Cè: conception and design of the article, writing of the manuscript
Natascha Claudia D'Amico: critical revision
Michaela Cellina: critical revision and final approval of the version to be submitted
References
- Shiina T, Nightingale KR, Palmeri ML, Hall TJ, Bamber JC, Barr RG, et al. WFUMB guidelines and recommendations for clinical use of ultrasound elastography: Part 1: basic principles and terminology. Ultrasound Med Biol, 2015; 41(5): 1126-1147. doi: 10.1016/j.ultrasmedbio.2015.03.009.
- Sigrist RMS, Liau J, Kaffas AE, Chammas MC, Willmann JK. Ultrasound Elastography: Review of Techniques and Clinical Applications. Theranostics, 2017; 7(5): 1303-1329. doi: 10.7150/thno.18650.
- Li GY, Cao Y. Mechanics of ultrasound elastography. Proc Math Phys Eng Sci, 2017; 473(2199): 20160841. doi: 10.1098/rspa.2016.0841.
- Greenleaf JF, Fatemi M, Insana M. Selected methods for imaging elastic properties of biological tissues. Annu Rev Biomed Eng, 2003; 5: 57-78. doi: 10.1146/annurev.bioeng.5.040202.121623.
- Parker KJ, Taylor LS, Gracewski S, Rubens DJ. A unified view of imaging the elastic properties of tissue. J Acoust Soc Am, 2005; 117(5): 2705-2712. doi: 10.1121/1.1880772.
- Wells PN, Liang HD. Medical ultrasound: imaging of soft tissue strain and elasticity. J R Soc Interface. 2011; 8(64): 1521-49. doi: 10.1098/rsif.2011.0054.
- Ophir J, Céspedes I, Ponnekanti H, Yazdi Y, Li X. Elastography: a quantitative method for imaging the elasticity of biological tissues. Ultrason Imaging, 1991; 13(2): 111-134. doi: 10.1177/016173469101300201.
- Shiina, Toshiyuki, et al. “Strain imaging using combined RF and envelope autocorrelation processing.” 1996 IEEE Ultrasonics Symposium. Proceedings, 1996; 2: 1331-1336.
- Varghese T, Ophir J. A theoretical framework for performance characterization of elastography: the strain filter. IEEE Trans Ultrason Ferroelectr Freq Control, 1997; 44(1): 164-172. doi: 10.1109/58.585212.
- Bamber JC. Ultrasound elasticity imaging: definition and technology. Eur Radiol. 1999; 9(3): S327-330. doi: 10.1007/pl00014066
- Hall TJ, Zhu Y, Spalding CS. In vivo real-time freehand palpation imaging. Ultrasound Med Biol, 2003; 29(3): 427-435. doi: 10.1016/s0301-5629(02)00733-0.
- Halliday D, Resnik R, Krane KS. Physics Vol. 1, 5th Edition, John Wiley. 2001; Wells PN, Liang HD. Medical ultrasound: imaging of soft tissue strain and elasticity. J R Soc Interface, 2011; 8(64): 1521-1549. doi: 10.1098/rsif.2011.0054.
- Hill CR, Bamber JC, ter Haar GR, (eds). Physical principles of medical ultrasonics. Chichester: John Wiley, 2004.
- Callister WD. Materials science and engineering: an introduction, 2nd edn. New York, NY: Wiley, 2000.
- Hall TJ, Zhu Y, Spalding CS. In vivo real-time freehand palpation imaging. Ultrasound Med Biol, 2003; 29(3): 427-435. doi: 10.1016/s0301-5629(02)00733-0.
- Doherty JR, Trahey GE, Nightingale KR, Palmeri ML. Acoustic radiation force elasticity imaging in diagnostic ultrasound. IEEE Trans Ultrason Ferroelectr Freq Control, 2013; 60(4): 685-701. doi:10.1109/TUFFC.2013.261.
- Nightingale KR, Palmeri ML, Nightingale RW, Trahey GE. On the feasibility of remote palpation using acoustic radiation force. J Acoust Soc Am, 2001; 110(1): 625-634. doi: 10.1121/1.1378344.
- Nightingale K, Soo MS, Nightingale R, Trahey G. Acoustic radiation force impulse imaging: in vivo demonstration of clinical feasibility. Ultrasound Med Biol, 2002; 28(2): 227-235. doi: 10.1016/s0301-5629(01)00499-9.
- He T, Peng B, Chen P and Jiang J. "Performance Assessment of Motion Tracking Methods in Ultrasound-based Shear Wave Elastography," 2020 IEEE International Conference on Systems, Man, and Cybernetics (SMC), 2020; pp. 3643-3648, doi: 10.1109/SMC42975.2020.9283024
- Shiina T, Nitta N, Ueno E, Bamber JC. Real time tissue elasticity imaging using the combined autocorrelation method. J Med Ultrason (2001), 2002; 29(3): 119-128. doi: 10.1007/BF02481234.
- Garra BS, Cespedes EI, Ophir J, Spratt SR, Zuurbier RA, Magnant CM, et al. Elastography of breast lesions: initial clinical results. Radiology, 1997; 202: 79–86.
- Gennisson JL, Deffieux T, Fink M, Tanter M. Ultrasound elastography: principles and techniques. Diagnostic and interventional imaging, 2013; 94: 487-495.
- Ricci P, Maggini E, Mancuso E, Lodise P, Cantisani V, Catalano C. Clinical application of breast elastography: State of the art. European journal of radiology, 2014; 83: 429-437
- Barr RG, Ferraioli G, Palmeri ML, Goodman ZD, Garcia-Tsao G, Rubin J, et al. Elastography Assessment of Liver Fibrosis: Society of Radiologists in Ultrasound Consensus Conference Statement. Radiology, 2015; 276: 845-861.
- GE Engineering. 2D Shear Wave Elastography LOGIQ E9/E10/E10s, 2020.
- Sandrin L, Fourquet B, Hasquenoph J-M, Yon S, Fournier C, Mal F, Christidis C, Ziol M, Poulet B, Kazemi F, Beaugrand M, Palau R. Transient elastography: a new noninvasive method for assessment of hepatic fibrosis. Ultrasound Med. Biol, 2003; 29: 1705–1713.
- Ferraioli G, Wong VW, Castera L, et al. Liver Ultrasound Elastography: An Update to the World Federation for Ultrasound in Medicine and Biology Guidelines and Recommendations. Ultrasound Med Biol, 2018; 44(12): 2419–2440
- Nightingale K, McAleavey S, Trahey G. Shear-wave generation using acoustic radiation force: in vivo and ex vivo results. Ultrasound Med Biol, 2003; 29(12): 1715-1723. doi: 10.1016/j.ultrasmedbio.2003.08.008.
- Sarvazyan AP, Rudenko OV, Swanson SD, Fowlkes JB, Emelianov SY. Shear wave elasticity imaging: a new ultrasonic technology of medical diagnostics. Ultrasound Med Biol, 1998; 24(9): 1419-1435. doi: 10.1016/s0301-5629(98)00110-0.
- Barr RG, Wilson SR, Rubens D, Garcia-Tsao G, Ferraioli G. Update to the Society of Radiologists in Ultrasound Liver Elastography Consensus Statement. Radiology, 2020; 296(2): 263-274. doi: 10.1148/radiol.2020192437.
- Friedrich-Rust M, Nierhoff J, Lupsor M, Sporea I, Fierbinteanu-Braticevici C, Strobel D, et al. Performance of Acoustic Radiation Force Impulse imaging for the staging of liver fibrosis: a pooled meta-analysis. Journal of viral hepatitis, 2012; 19: e212-219;
- Ferraioli G, Tinelli C, Dal Bello B, Zicchetti M, Filice G, Filice C, et al. Accuracy of real-time shear wave elastography for assessing liver fibrosis in chronic hepatitis C: a pilot study. Hepatology, 2012; 56: 2125-2133.
- 30-2Itoh A, Ueno E, Tohno E, Kamma H, Takahashi H, Shiina T, et al. Breast disease: clinical application of US elastography for diagnosis. Radiology, 2006; 239(2): 341-350. doi: 10.1148/radiol.2391041676.
- Goodman ZD. Grading and staging systems for inflammation and fibrosis in chronic liver diseases. J Hepatol, 2007; 47(4): 598–60733.

