Wrong Physiological Concepts Pervading Clinical Management of Arterial Pressure Physiological and Bayesian Concepts in Arterial Hypertension
Alejandro Alonso-Altamirano1, Daniel Lamothe2, Rabindranath García-López3,4, Estuardo Hernandez-Coria5,6, Francisco Guillermo Castillo-Vázquez7, James Morey8, Nery Lamothe9, Mara Lamothe9
1Coordinator of Internship and Social Service of the Medical Surgeon Career. Full-time professor and Researcher Universidad Autónoma Metropolitana. Xochimilco
2Universidad Westhill, Escuela de Medicina, Mexico
3Departamento de Neurocirugía, Hospital de Especialidades Centro Médico Nacional Siglo XXI, Ciudad de México, México
4Centro Neurológico ABC, Centro Medico American British Cowdray (ABC). Ciudad de México, México
5Orthopaedic Service of the General Hospital of Iztapalapa
6High Specialty in Joint Surgery, UNAM, Mexico
7Staff physician, Department of Orthopaedic Surgery, The American British Cowdray Medical Center, México City
8Medical Student in Dnipro DMI, Surgery Dept Ukraine
9División de Ciencias Biologicas y de la Salud, Medical Surgeon Career, Universidad Autónoma Metropolitana, Xochimilco, Mexico
Received Date: 25/06/2022; Published Date: 04/07/2022
*Corresponding author: Nery Lamothe, División de Ciencias Biologicas y de la Salud, Medical Surgeon Career, Universidad Autónoma Metropolitana, Xochimilco, Mexico
Summary
Wrong physiological beliefs about hypertension in surgery and medicine, constituting conceptual atrocities:
1. Many physicians believe that perfusion decays with the fourth power of the radius, which is a doxastic misunderstanding of the Poiseuille equation.
2. In the occlusion of an artery, often, instead of the radius, they measure the cross-sectional area.
3. If we reduce the driving pressure with antihypertensive drugs, we are decreasing axial pressure and in turn perfusion.
4. Taking clinically the blood pressure, we measure transmural instead of driving pressure which is what generates perfusion.
5. The principal hemodynamic etiology of damage is not transmural hypertension but instead is the Laplacian tension.
6. The pathogenicity of the arteries is not depending on transmural pressure but instead on the energy density per unit of time, measured in Joules per cubic meter, per second, or in Watts per cubic meter.
7. Hypertension, in a strict sense, increases perfusion.
8. The baroreceptors do not respond to the transmural pressure but instead to the Laplacian arterial tension, which corresponds to arterial distention.
9. The brain tissue, as well as the cardiac tissue, possess self-regulation machinery for their perfusion, however vasodilators increase perfusion in most tissues, diminishing neural and coronary perfusion as a stolen effect.
10. All gradients consist of potential energy, as is the case in pressure, or electricity.
11. The time derivative of pressure, is the change in pressure as a function of time, it is the differential of the work per volume per time; a change in work density due to time, which is power density.
12. The determinant of perfusion is the axial gradient, not of pressure gradient but of an energy gradient.
13. As a hyperbolical approach, if we take the pressure of an elephant, we would certainly obtain higher readings.
14. The pressure is, strictly, energy density, or energy per infinitesimal unit of volume.
15. The venous return of blood is the volume of blood flow returning to the right side of the heart. The input of the right side must be equal to its output, thus, in the steady-state situation, the cardiac output from the right and left sides are equal. In consequence, the systemic venous return has to match the systemic cardiac output. Venous return must be equal to or less than the cardiac output. The heart, considered as a pump, is unable to expel a volume that has not been received; however, in the case of valve regurgitation, the heart might expel a fraction of the venous return twice. Thus, the clinician must answer the question: Is the preload volume in the end-diastolic volume EDV or the pressure at the instant of the EDV that has diminished before the initiation of the isovolumic contraction?
Introduction
Ignoring the concepts analyzed here are the causes of at least fifteen types of dramatic errors in the diagnosis and management of arterial hypertension.
In the mathematical aspects, the reader may, if he considers himself an expert, verify that they correspond to the paradigm; if not, on first reading he may conditionally accept the mathematical physical implications and continue; at another time, he can review the mathematical foundations, which are here to give light to the concepts and not as superfluous aesthetic elements. The approach consists in the application of the Popperian refutative procedure, considering all the mathematical logical results as protocol clauses [1]; considering them in a conditional logic: if the mathematical inferences result consistent and without contradictions; then, the physiological and clinical tragedies are demonstrated. The biophysics of the cardiovascular system strictly obeys the biophysical laws.
The function to be optimized is to decrease the effect of hypertension [2]; alternatively, the function to be optimized in surgical patients is to obtain adequate perfusion and oxygenation to the brain, heart, etc. during the surgical procedure as well as in the and in the perioperative time.
Beyond optimizing the surgical repair, it is transcendental to avoid the tragedies of hypoxia and ischemia to which the surgical patient is especially susceptible. These surgical situations are not the moment to avoid hyaline arteriolosclerosis nor avoid concentric hypertrophy of the left ventricle resulting from increased afterload pressure. Attention should focus on oxygen availability for the mitochondria and perfusion [3-8].
The dream in an ideal eutrophic perfusion model is fallacious. Evolution is the result of random variation and the selection of genotypes through their phenotypical expression in terms of the reproductive success of selfish genes. This is not an ideological position, but a description of the evolution of the genes. Alternatively, we can study the doxastic logic and the desiderative logic in the dogmatic texts as is the case in the following example: [9] “The morphology and local regulatory mechanisms of the microcirculation are designed to meet the particular needs of each tissue” [10]. Also, taken from the highest respected textbook of cardiology, “Braun Wald’s Heart Disease”, you can read: “the endothelial lining of blood vessels is critical to vascular health and constitutes a major defense against hypertension” [2,11].
This constitutes a tragic teleology!!!
We can take the time derivative of pressure:

The driving (axial) pressure between two points is the pressure gradient of those points in the vessel. This is the pressure that is on the above equation and it is completely different from the transmural pressure. Physical damage to the endothelium, hyaline and hyperplastic arteriolosclerosis, and the hemorrhagic rupture of vessels, are all due to the instantaneous Laplacian tension, which is the power per unit area, rather than transmural pressure as measured by a sphygmomanometer, given that the mathematical theory of catastrophes predicts the behavior of the system.
Here we refer to pressure as the driving pressure, which means the difference between the pressure taken at two different points in the trajectory of a vessel.
In terms of Bertalanffy's General Systems Theory [13], the meta-topological structure of the cardiovascular system changes as a function of time and the organizational level. To understand the biophysical consequences, perfusion and arterial pressure as a subrogate in surgical and clinical management, we need to turn our attention to thermodynamics, diffusion, and convection. As it is the case that the equations of Poiseuille and Bernoulli are subsumed in the Navier-Stokes’s equations, through the lambda extractor, we consider them as such [14].
Pappenheimer improved the classical model of absorption and filtration by Starling; however, a better version of this has come up isolating the subglycocalyx fluid and its space [10].
Also, the same way as the equations of Poiseuille and Bernoulli are subsumed in the Navier-Stokes’s equations, through the lambda extractor, it is also true for the Fick’s equation [15].
Leibniz´S Mathesis and Apodicticical Equation Derivations
Convective perspective
In the cardiovascular system, there are three convective loops: The transportation of blood, the filtration absorption transcapillary wall, and the circulation of lymph [7].
The convection enlarges the gradient, increasing the diffusion due to, thermodynamically, blood on the one side and atmospheric air on the other, functionally behaving as quasi-infinite reservoirs [13].
In the capillaries, the diffusion obeys Starling's law of equilibrium; however, convection obeys the Navier-Stokes’s equations, which here we integrate with respect to distance, in every, so we change from units of force/volume to the energy/volume.
Navier Stokes equations
Dimensional Analysis [12]


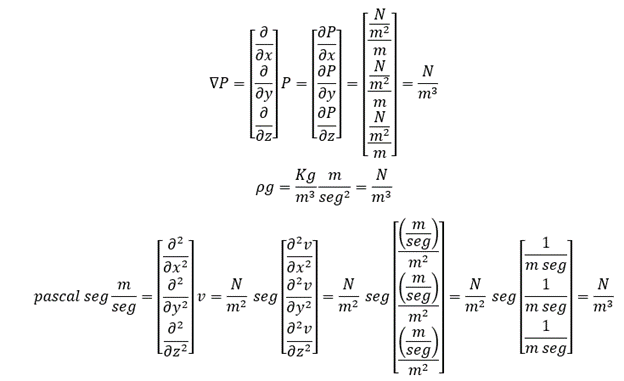
We have to follow the dimensional analysis in each step of the derivation.
We need to make sure that both sides of each of the three equations are in units of force per volume (N/m3).
In the first equation, the first term in the left side is , which is density multiply times the time partial derivative of the component in the x direction of velocity, those the units are (kg/m3) [(m/seg)/seg] = (kg/m3) (m/seg2) = N/m3, or units of force per volume.
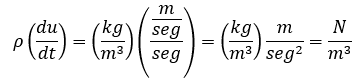
In the first equation, second to fourth terms of the left side of the equation, we have density times the x component of the velocity times the partial position partial derivative of velocity in x direction with respect to the x, y or z directions.

First equation, right side, first term: density times gravity acceleration in the x direction:
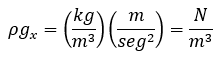
First equation, right side, second term: the x directional derivative of pressure.

First equation, right side, third to fifth terms: viscosity, multiplied by the second partial positional derivative of velocity.
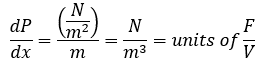
If we integrate both sides of the three equation of Navier-Stokes, respectively, with respect to dx, dy or dz, we get units of newtons per square meter, N/m2 which are units of pressure. Multiplying by a convenient one, m/m, the unit become joules per cubic meter, J/m3 or energy density p [12].
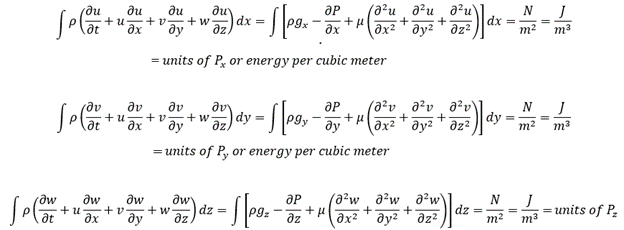
Iterated integration of the original equations of Navier-Stokes with respect to dx, dy and dz, leave us with force units, Newtons:

Momentum conservation:
We now integrate both sides with respect to time, obtaining units of impulse (force times time) or momentum units 12].
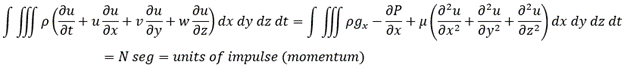
Mass conservation:
Dividing the previous equations (those with three iterated integrals), which have a unit of force, by the acceleration of gravity, results in mass conservation.
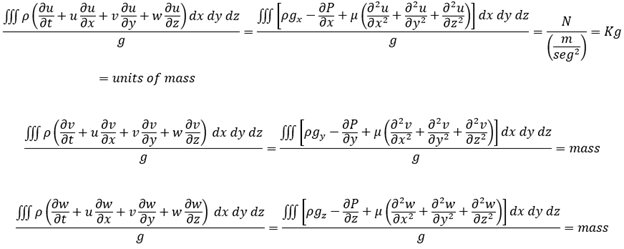
We can equate the previous three equations with each other because of mass conservation.

We have to recognize that in the equations of Navier Stokes, even though it is known the initial conditions, there is not a prediction of the system, in part, because of a nonpolynomial problem. We can have a system that is homogeneous at a given level, however, this homogeneity is not true for the molecular level, where there is heterogeneity; as such, what is true for a given level may be not to: “at different levels, there are different properties”. even though this does not give us exhaustively the conditions of every and each minimum minimmorum amount volume, we need to determine the initial conditions statistically, either by, Lagrangian or Eulerian perspective [12].
A factor that increases the unpredict ableness of the system, is the fact that Lorentzian chaos is produced by the unmeasured components that constitute points of synergetic fluctuation [15].
Since there is no way to isolate the system, the conditions of the system are continuously changing, because of the incommensurable effects the surrounding has over the system.
Each method we use to measure a property of the system, implies a disturbance to the system, per se by doing the measure and altering as such the conditions of the system, at least we have to deal like this, with the uncertainty principle of Heisenberg [12].
“Keep science as simple as possible, however, no more than what it is possible”, as an Einsteinian argument, is despised in several science aspects where there is an intrinsic difficulty of the Res (concept) per se, as there cannot be explained as simpler than what is possible; and this is also true for the concept of Navier Stokes equations.
The overcompensation that occurs as part of a homeostatic process when there is a disturbance, is evidence of the hysteresis property the homeostatic mechanisms have [13].
There is a continuous gradient for both gasses O2 and CO2, which determines the direction of each gas, in terms of the law of Fick and Starling, since blood is an anisotropic medium, and also it is it in different ways for each gas. For the O2, alveoli acts as a source of O2 and blood acts as a sink for molecular oxygen, since there is more O2 in the alveoli compared with the one in the blood; in the other hand, for the CO2, alveoli act as a sink of CO2, and blood as a source of carbon dioxide, because there is less CO2 in the alveoli compared with the blood; all this in terms of a vector field and accentuating this effect by several orders of magnitude, by the convection that is generated by the bulk movement, which is produced on one side by the movement of the blood on each beat of the heart, and also on the other side, for the bulk movement of the gasses in each breath in the respiratory tract.
Life is possible because of the increasing entropy consuming O2 and producing CO2 in the mitochondria18. It also depends on the exponential chaos that is created by the action potential at the moment of sodium entering the cells, the positive feedback, and in the production of turbulence of both: the gasses (O2 and CO2) and liquid (blood), obeying Navier-Stokes equations [13].
By the same token, in an isomorphic manner, the same happens with nutrients and waste products. Making analogy of this example with the previous one of the gasses: the nutrients analogous with the O2, the intestinal lumen analogous with the alveoli, the waste products analogous with the CO2, and the light of the blood vessel analogous with the mitochondria on the cells in which CO2 is produced and released in the blood; as such, in one hand side the luminal membrane of intestinal epithelia acts as a source of nutrients while the light of the vessels acts as a sink for waste products, and on the other hand side, the luminal membrane of intestinal epithelia acts as a sink for waste products while the light of the vessels acts as a source for waste products. This is because of the fact that there are more nutrients on the lumen of the gut than in the light of the blood vessels and there is more waste product in the blood vessel than in the lumen of the gut. All this following Fick’s laws and the convection generated by the movement of the blood with each heartbeat and convection produced by the movement of the gastrointestinal content on each peristaltic wave, translating this effect into turbulence and chaos, also in the frame of Navier-Stokes’s equations and the Lorentzian chaos [13].
As previously said, life exists because of entropy, but also because of the thermodynamic advantage of decreasing the entropy of the system which is being studied, at the expense of increasing a lot more the entropy of the surrounding of the system, thus making order from chaos without violating the second law of thermodynamics. Meaning, it creates anabolism because the created order is done at the expense of energy obtained from the nutrients (surrounding) and molecular oxygen generating combustion and releasing energy from the exterior sources [16].
Thus all energy is derived from the capture of sunlight, and this capture is done at the cellular level in the chloroplast of the plants, following Shannon's mathematical theory of communication, defined as the negative base 2-logarithm of the possible microstates, which is done without design, cybernetically, due to information [17].
On the same line of thoughts, there are many nephrons acting as a sink for the vector field corresponding to waste products
Diffusion
Fick´s law of diffusion

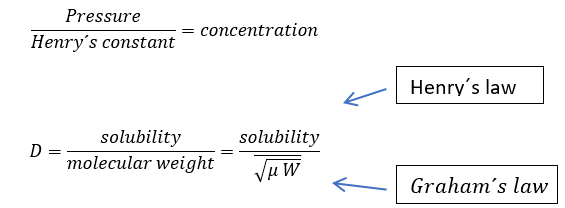
d Desiderative Logics
Doxastic and apophantic logic. The doxastic logic and the desiderative logic are the two matrix components of the decisional logic. Apodictic logic is an inference that is mandatory, doxastic logic, once the axioms are tentatively accepted (doxastically) true [19].
An estimation of the risk is a belief (which is doxastic logic), vs, on the other hand, benefits which are de facto being this desiderative logic. These are the matrix components of the logic of a decision. We need to avoid that medical practice being subsumed, by a lambda extractor to the Nash equilibrium, converging a doxastic logic in terms of false belief, and a desiderative logic, in terms of unreachable desires [19].
Bayes Mathematical Theorem
Hypertension, previously viewed as an abnormal variation of a physiologic parameter that increases the risk of morbimortality. On the one hand, especially if there is poor understanding of the physiopathological components, applying Bayes theorem may guide to false assumption; however, on the other hand, the failure to apply this mathematical theorem, which is pervasive not only in criminal law but also in all experimental science and medicine, will guide us to a tragedy at decision-taking moment [21]. Formally:
Delta (Δ) is a probability space, where we can define a sigma-algebra of events, with a probability measure. Delta would be composed of all the events of A, that is, it is a partition of the sample space that is formed by all the people with symptoms, and “De =” is an event that is intersecting the events of delta, therefore we can calculate conditional probabilities and apply Bayes' theorem [22,23].
If Δ={De: e J} is any class of mutually exclusive countable events,
De = Disease
A = Abnormal result in the test
Dj = No disease
P() = Bayesian Probability Function
If A is any abnormal test result with positive such that
then:
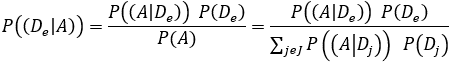
Chaos Vs Catastrophes
The discovery by René Thom of the impact that abrupt changes have given rise to the so-called mathematical theory of catastrophes as a branch of mathematics; as such awarding him the highest prize in the mathematical field [24], the Fields Medal.
The transition from two different states of affairs, when this occurs in a paroxysmal manner, constitutes a Catastrophe, which has a Boolean behavior, corresponding to, on one hand, before it happens the sudden transition, and on the other hand, after it has occurred. Because of the decay of metastable energy, this paroxistic transition can appear. On the contrary, the energy that allows chaos propagation, for example in the dominos reactions, is the released energy by every new element captured by the chaotic phenomenon15, behaving in a continuous exponential or logistic growth [15].
Some examples of an instructive type of catastrophic phenomena are [24]:
- lighting
- alpha, beta, and gamma nuclear decay
- phosphorescence
- the release of oxygen from hemoglobin
- death is a catastrophic event
- the entrance to sleep
- ovulation
- the latch locks
- the all or nothing law of synaptic transmission
- the boiling of water
- the explosion of soap bubbles
- balloons, balls, and tires, camels' backs broken when overridden
- the emission of photons and electrons
- the double-loop hairpin that goes off, the laughter, the atomic pen
- the Kuhnian reconfiguration
- sensory identification: hearing
- sight, smell, taste, popcorn
- breaking a potato chip in the mouth
- dripping, Buridan's ass decision
- the decisional process, the steps of a Turing machine
- hiccups, the sneeze
- the production of a thymine dimer
- the bifurcation of the vessels, the vision, the glacier detachment, the breaking of the glass, the equation: Y = a / (x-b)
Lorentzian Chaos is an exponential function, Thom's catastrophe is the function of a hyperbola y = a / (x-b) at the point where x is equal to b15.
Kolmogorov´s Microscales of Turbulent Flow
Regarding turbulent flow, the smallest scales are those of Kolmogorov, called Kolmogorov microscales. Here, there is dissipation of energy into heat and the predominant parameter is the viscosity [15].
In Kolmogorov´s conception of turbulence, the smallest scales depend only on 𝜈 (nu, kinematic viscosity) ε (epsilon, the average rate of dissipation which is viscosity per density) and are universal, from kilometers to less than a millimeter for length scales [15].
Dimensional analysis Kolmogorov´s Microscales:

The True interpretation of Poiseuille Law [13]
If we increase the resistance in a blood vessel, the pressure before the resistance increases, and the pressure after the resistance decreases, then the pressure gradient increases. The blood cannot pass from before the resistance to after it because of this increase in the pressure gradient that favors the blood passing from before the resistance to after it.
This is because the pressure changes with the square power of the radius because the pressure is force divided by area. As we all know from Poiseuille's Equation, the resistance varies with the inverse of the fourth power of the radius, therefore when the radius is decreased by half, the pressure gradient decreases by 50%, the resistance increases by a factor of 1/16, and flow, which is pressure gradient divided by resistance decreases by 50%, not by a factor of 1/16. The radius changes with the second power of the radius, not the fourth power.
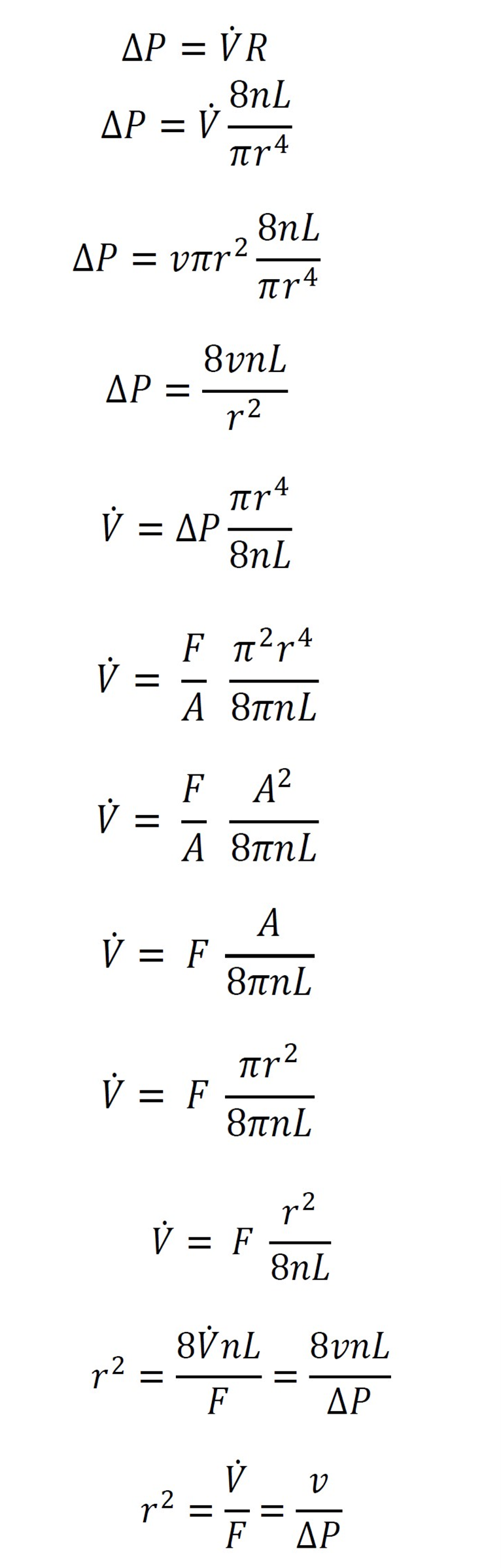

Mathematical Theory of Queues [25] and Thermodynamics First Law Impede that the Venous Return Decreases
Systole begins with the contraction of the ventricle, which closes the atrioventricular valves, and as ventricular contractions increases, so the pressure inside the ventricles; when this pressure is slightly more than the pressure of the aorta (or the pulmonary artery talking about the right ventricle), the semilunar valves open, being the aorta and left ventricle (or pulmonary artery and right ventricle) topologically the same cavity as long as the semilunar valve is open. Now being the ventricle and aorta the same cavity, the pressure of the left ventricle continues to increase as the muscle contracts until it reaches its maximum value corresponding to the systolic blood pressure (about 120 mmHg). Then the ventricle, which continues to be in communication with the aorta, relaxes decreasing the pressure of both the ventricle and the aorta, allowing very little blood to pass from the aorta to the ventricle, and as blood from the aorta pushes the leaflets of the aortic valve then it closes. As this goes on, the ventricle then contracts again, and as soon as its pressure is slightly above the aortic pressure the semilunar valves open, corresponding to the smallest pressure the aorta artery has, being the diastolic blood pressure. So, the value of the diastolic blood pressure is determined by the blood going to the branches of the aorta and then their capillaries and the pressure generated by the ventricular contraction. When taking the blood pressure with the sphygmomanometer is the maximum transmural pressure in systole and diastole. So now suppose the left ventricle contract shortly after the end of systole, meaning that soon after the systole, the aortic valve will open, being this a higher diastolic blood pressure value than if the aortic valve would not have opened so quickly, because there have not has happened enough time for blood to hoes into capillaries and for left ventricle pressure to comes down. So as an apodictic inference, diastolic blood pressure rises in tachycardia (where soon after systole then the ventricle will contract again), and diastolic blood pressure decreases with bradycardia [8].
If it is the case that the heart stops pumping the blood, by Newton's first law, the blood still is moving inertially in a hysterical manner, until a force modified it, being this when the energy gradient disappears, corresponding to the equilibrium point. Here axial pressure is 0 and the transition of the whole system in just one communicated space is the axial meta-topology, however paradoxically, since the cardiovascular system still contains blood expanding the vessels, it has been inflated to 7 mmHg, this value being called the Mean Systemic Filling Pressure.
Given the elastic property of the aorta artery and arteries wall, the aortic pressure increases because of the storage of potential energy in the aortic wall before the blood goes from the aorta to the capillaries, as ventricle contracts; however, finally, blood will enter the capillaries as elastic potential energy is lost from the arterial walls [8].
Following the same line of thought as George L. Brngelmann:
“Perhaps in many situations, physicians have made correct interventions based on the idea that mean systemic pressure drives venous return26. However, reaching the right answer for the wrong reason constitutes a mixture of intuition with luck”
We will get more information about how the venous return influences cardiac output if we move to empower with knowledge and understanding of how blood volume results apportioned in the topological space that constitutes the cardiovascular system given because of their energetic gradient.
Laplacian Tension (Not Transmural Pressure)
Laplace law:

Units of k are:

Wall tension:
Dividing by length
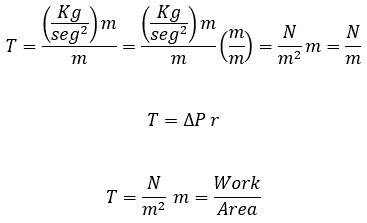
Bernoulli Equations
Now we can see that pressure and velocity are inversely related.

If the fluid is static, the velocities are equal to zero:
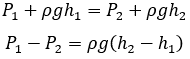
Power in Bernoulli equation

Momentum in Bernoulli equation
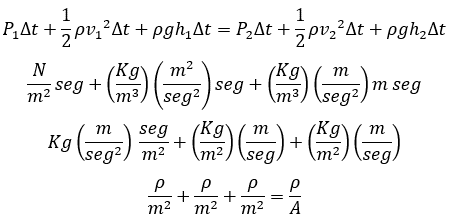
Blood flow is determined by Bernoulli equation in terms of energy, not pressure [13].
Equation of motion:

Newton's second law [30,31]:
We usually accept that in vessels, the flow goes from higher pressure to lower pressure. This is wrong, fluid flow is determined by the change in energy, so that fluid flow is from a higher to a lower total energy (kinetic and potential energy, which are composed of pressure, seen in Bernoulli equation) level [10].
Consider a blood vessel with a narrower region in the middle compared to its extreme ends, as shown in figure 1. Remember the continuity equation, which states that the cross-sectional area multiplied by the velocity in any region of the vessels is constant; therefore, the narrower segment has a higher velocity than that at the extreme ends.
The narrower region indeed has lower potential energy, in this case, 60 mmHg, than the extreme ends, it has much more kinetic energy because kinetic energy has the term of velocity squared in it.
Therefore, the narrower segment has the greatest mechanical energy (potential plus kinetic energy) and flow.

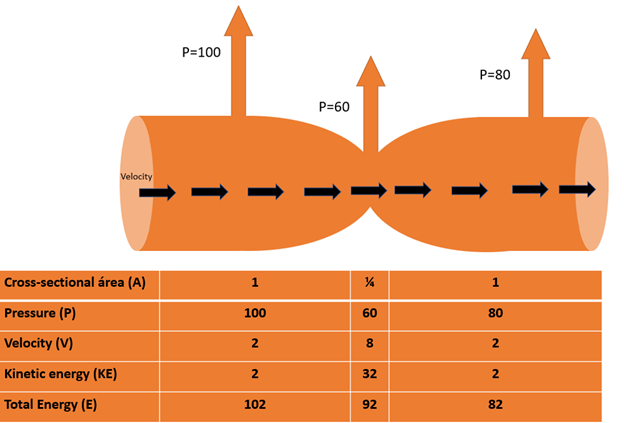
This is an instance of a reversible conversion between pressure, which is potential energy10, and velocity which is kinetic energy, because velocity changes along the length of a vessel even though the blood flow is constant. These changes in velocity contribute to the changes in pressure inside the aorta.
Energy in Bernoulli equation
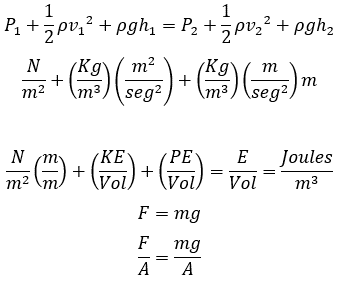
Given that
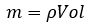
Then:
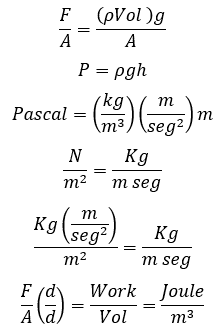
Since a low-pressure system has the potential to do work in the surrounding medium, then, it is evident that pressure is a measure of potential energy stored per volume. Pressure is therefore related to energy density and can be expressed in units such as Joules per cubic meter; Which is mathematically equal to the Pascal unit.
Integral of momentum whit respect to velocity is kinetic energy:
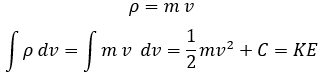
Particle and Bulk movement [13].

Conclusion
Blood flow is determined by the energy gradient and not the pressure gradient [8].
What moves gasses across the blood and alveoli is the convection in the capillary and alveoli and not the diffusion of gasses. Paradoxically it is the entropy [8].
Compare Axial Meta-topology vs. Transmural Meta-Topology giving rise to Disquisitions about Vascular Meta-topology [32].
Is the dynamic surgical topological transformation of the cardiovascular system between systole and diastole that constitutes an axial meta-topology. A set of techniques to create one finite-dimensional manifold starting from another [32] is Milnor´s surgery theory, in a background of mathematics, especially in geometrics.
During diastole, the cardiovascular system is divided into two topological spaces which constitute32:
- pulmonary circuit
- pulmonary artery
- pulmonary capillaries
- pulmonary veins
- left atrium
- left ventricle
- systemic circuit
- aorta
- systemic arteries
- systemic capillaries
- venules
- cava veins
- right atrium
- right ventricle
In systole, the cardiovascular system is divided into another different two topological spaces which constitute [32]:
- systemic circuit:
- left ventricle
- aorta
- systemic arteries
- systemic capillaries
- venules
- cava veins
- right atrium
- Pulmonary system:
- right ventricle
- pulmonary artery
- pulmonary capillaries
- pulmonary veins
- left atrium
There are topologically 4 cavities in the cardiovascular system at the moment of isovolumetric relaxation and isovolumetric contraction are which corresponds to the following cavities:
- left ventricle
- right ventricle
- the whole cavity form from the pulmonary artery to pulmonary capillaries to pulmonary veins to the left atrium
- the whole cavity form from the aortic valve, systemic arteries, systemic capillaries, venules, cava veins until the right atrium
There are 4 moments in which the topological space of the cardiovascular system abruptly change, being a catastrophic point:
- closure of mitral and tricuspid valve
- opening of the aortic valve and pulmonic valve
- closure of the aortic valve and pulmonic valve
- opening of mitral and tricuspid valve
Meta-Topology [32]
The cardiovascular system has different topological spaces that depend on the time of the cardiac cycle in which we are analyzing it and at which structural level we are considered (cellular like red blood cells, proteins like hemoglobin, molecules, water, gasses, and electrolytes.
The movement of fluids, air, or water, for example, is a bulk movement or convection. The movement of solutes is diffusive, hence in a blood vessel, the movement of water is determined by capillary convection and that of solutes by transcapillary diffusion.
We are at the expectancy of a Popperian refutation, in the meantime:
We end this paper with an invitation to the academical community to refute, apodictically, epagogically or empirically, what we have concluded. Critical comments, if not refutative, will be considered as weak doxastic or desiderative attitude. All that has been said, are so, in terms of a Newtonian dictum: Hypotheses non fingo.
quod erat demonstrandum
References
- Popper K. The Logic of Scientific Discovery. , Routledge: Great Britain. Ref.: 2002.
- Ronald V. Systemic Hypertension: Mechanism and Diagnosis in Mann, Zipes, Libby, Bonow. Braunwald's Heart Disease. Canada. ELSEVIER. 11 Ed, 2019.
- Lamothe N, Lamothe M, Lamothe D, Lamothe P, Hernández-Garcia A. Application of the Parsimony Principle of Exponential Functions to the Production of COVID-19 Immunity, according to Bayesian Theorem and Cybernetics, to Tame Anti-scientific Doxastic Logic and the Pandemic. International Journal of Biology And Medicine, 2020; 33-47.
- Lamothe N, Lamothe M, Lamothe D, Sierra C, González- Téllez-Girón CH, et al. Bayesian Model for Covid-19 to Achieve Immunity by Parsimony of Exponential Functions Minimizing the Inoculum. J Emerg Dis Virol, 2021; 6(1): dx.doi.org/10.16966/2473-1846.160
- Lamothe M, Lamothe N, Lamothe D, Hernández-Garcia A, Castillo C, et al. Exponential Parsimony to Generate Herd Immunity Against SARS- CoV2 Cybernetically Restricting Doxastic and Desiderative Logics. International Journal of Coronaviruses, 2021; 2(3): 11-22.
- Sánchez-Hernández JP, Frausto-Solís J, González-Barbosa JJ, Soto-Monterrubio DA, Maldonado-Nava F G, Castilla-Valdez G. A Peptides Prediction Methodology for Tertiary Structure Based on Simulated Annealing. Math. Comput. Appl. 2021; 26(2): 39.
- Frausto-Solís J, Hernández-González LJ, González-Barbosa JJ. Convolutional Neural Network–Component Transformation (CNN–CT) for Confirmed COVID-19 Cases. Mathematical and Computational Applications, 2021; 26(2): 29.
- Canul-Reich J, Frausto-Solís J, Hernández-Torruco J. A predictive model for Guillain-Barré syndrome based on single learning algorithms Computational and mathematical methods in medicine, 2017.
- Richard Dawkins, Selfish genes. Oxford England. Oxford University Press, 2016.
- Boron WF, Boulpaep EL. Medical Physiology. China. Elsevier. 3 Ed, 2017.
- Fauci AS, Hauser SL, Longo DL, Jameson JL, Loscalzo J, Kotchen T. Hypertensive Vascular Disease in Kasper DL, Harrison’s Principles of Internal Medicine. 19a Ed. USA: McGraw-Hill Education. 20 Ed, 2018.
- Giles RV, Evett JV, Liu C. Schaum´s: Fluid Mechanics and Hydraulics. USA. McGraw-Hill, 1994.
- von Bertalanffy. General System Theory: Foundations, Development, Applications. George Braziller Inc., 2015.
- Potter MC, Wiggert DC. Schaum´s: Fluid Mechanics. USA. McGraw-Hill, 2021.
- Hughes W, Brighton JA. Schaum´s: Fluid Dynamics. USA. McGraw-Hill, 1999.
- Atkins P, de Paula J. Physical Chemistry. Great Britain. Oxford University Press. 9 Ed, 2010.
- Thorne KS, Blandford RD. Modern Classical Physics. United Kingdom. Princeton University Press, 2017.
- Principles of Biochemistry. USA. W. H. Freeman, 7 Ed, 2017.
- Shannon C. The Mathematical Theory of Communication, USA, 1949.
- Neuhauser C. Calculus for biology and medicine. USA. Pearson Prentice Hall. 2 ED, 2004.
- Jeffrey RC. The Logic of Decision. 2 Ed. USA. The University of Chicago, 1965
- Giroux É. Epidemiology and the bio-statistical theory of disease: a challenging perspective. Theor Med Bioeth. 2015; 36(3): 175-195. doi: 10.1007/s11017-015-9327-7. PMID: 25951975
- Mark DBy, Wong JB, en Jameson J. The Practice of Medicine in Kasper DL, Fauci AS, Hause SL, Longo DL, Jameson JL, Loscalzo J. Harrison’s Principles of Internal Medicine. 19a Ed. USA: McGraw-Hill Education. 20 Ed, 2018.
- Lamothe M, Lamothe N, Lamothe D, Lamothe P. La tragedia bayesiana desde la iatrogenia clínica hasta la biotecnología. Revista Médica Del Instituto Mexicano Del Seguro Social, 2017; 55(5): 641-659.
- Lamothe N, Lamothe M, Lamothe P, Lamothe D, Altamirano A. Bayesian Tragedy and Categorical Medical Error in Prostate Cancer. Global Journal of Urology, 2019; 20-28. doi: 10.36811/gju.2019.110004.
- Poston T. Stewart I. Catastrophe Theory and Its Applications. USA. Dover Publications, 1978.
- Lamothe PJ. Reforma de los Estados Democráticos y de los Oclócratas. México: Primer Mandante Epistemócrata de los Estados Unidos Mexicanos, 2007.
- Brengelmann GL. Venous return, mean systemic pressure and getting the right answer for the wrong reason. Annals of Translational Medicine, 2019; 7(8): 185. doi: 21037/atm.2019.03.64.
- Parati Gianfranco, Bilo Grzegorza, Mancia Giuseppe. Blood pressure measurement in research and in clinical practice: recent evidence, Current Opinion in Nephrology and Hypertension: 2004; 13(3): p 343-357.
- James GD, Gerber LM. Measuring arterial blood pressure in humans: Auscultatory and automatic measurement techniques for human biological field studies. Am J Hum Biol, 2018; 30: e23063.
- Herman IP. Physics of the Human Body, Springer.
- Serway RA, Beichner RJ. Physics for Scientists and engineers. USA. Saunders College Publishing, 5 Ed, 2000.
- Sears Zemansky. University Physics. USA. Pearson-Addison Wesley, 12 Ed, 2008.
- Lipschutz S. Schaum´s: General Topology. USA. McGraw-Hill, 2012.

